Top 4 Foundational Model Drawing Skills for Lower Primary
Basic model drawing skills for solving problem-solving heuristics
Model drawing provides an important foundation for students to build upon as they learn more challenging problem-solving heuristics at the upper primary level. Without a strong foundation in model drawing, many students struggle with mathematical problem sums. Model drawing is essentially like creating a picture of the maths problem. It helps students visualise the numbers and language in word problems more clearly and meaningfully.
Here’s how it works:
Analyse the question carefully
Identify the clues and key words in the question
Draw the model to represent the problem
Turn the words and numbers into pictorial form (Models) so that it is easy to
visualise and solve
In this article, we’ll take a closer look at 4 types of models, each suited to specific kinds of maths questions.
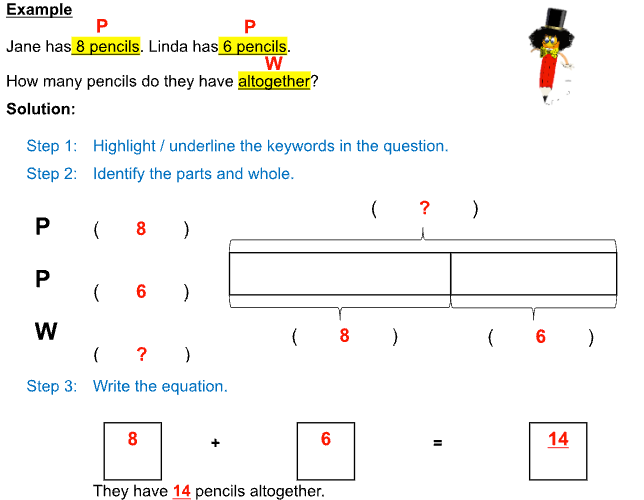
Part-Whole Model : How A Whole Can be Split Into Parts
This model is based on the concept that a whole (W) can be divided into smaller parts (P). By understanding this relationship, students can better grasp the connection between addition and subtraction.
By visualising how parts come together to form a whole, or how a part can be found from the whole, students gain a clearer picture of the mathematical relationships involved. This model encourages students to look out for clue words such as “altogether,” “total,” “in all,” and “left”—these signal the suitability of using the Part-Whole approach.
Unitary Model: Forms the Foundation For Other Model Types
The Unitary Model is a fundamental technique in model drawing, upon which various other models such as the Comparison Model and Before & After Model are based.
This model represents quantities using equal units, making it especially useful when one quantity is a multiple of another, or when a total value is shared equally across units. It helps students visualise and solve problems involving multiplication, division, and ratios in a clear, structured way.
Clue words that suggest the use of the Unitary Model include phrases such as “twice as many,” “three times as much,” or when a question gives a total for several equal parts.
Comparison Model: Comparing Two Or More Quantities
A strong grasp of the Comparison Model helps students avoid common misconceptions—such as thinking that the word “fewer” always means subtraction or that “more” always calls for addition. Instead, the model encourages students to first understand the relationship between the quantities before deciding on the operation needed.
Students should look out for clue words like “more than,” “less than,” “fewer,” “taller,” “shorter,” and “difference”, which often indicate the use of a Comparison Model.
Before & After Model: Brought About a ‘Before’ and ‘After’ Situation
This model helps students visualise what happened before and after a change takes place and is particularly helpful when a quantity is added, removed, shared, or shifted between parties.
To accurately represent the scenario, students may need to draw two separate models—one for the initial state and another for the final state—or modify a single model to reflect the changes accordingly. This allows students to track the transformation clearly and determine the unknown values involved.
Final Thoughts
Mastering the fundamentals of model drawing is an essential step in building a strong mathematical foundation for students in their early years. As students progress to upper primary levels, they are increasingly expected to tackle more complex and layered problem sums. With a solid grasp of model drawing, they will be better equipped to make sense of these challenges.
Model drawing enables students to visualise quantities and their relationships, allowing them to confront word problems with a structured and strategic mindset. This approach becomes especially valuable when students encounter advanced topics such as fractions, ratios, and percentages—where representing parts of a whole and comparing proportional values are key.
It also supports the development of algebraic thinking, as the bar representations in model drawing closely resemble the use of variables to express unknowns, easing the transition to more abstract concepts.
For multi-step or complex word problems, model drawing provides a reliable framework to break down the information, map out the steps required, and solve the problem logically.
Explore more ways by which model drawing supports mathematical thinking with our related post, where we unpack additional strategies to strengthen problem-solving skills.